이번에는 오랜만에 이분 탐색 태그가 달린 문제를 풀어봤습니다.
1300번: K번째 수
세준이는 크기가 N×N인 배열 A를 만들었다. 배열에 들어있는 수 A[i][j] = i×j 이다. 이 수를 일차원 배열 B에 넣으면 B의 크기는 N×N이 된다. B를 오름차순 정렬했을 때, B[k]를 구해보자. 배열 A와 B
www.acmicpc.net
난이도가 골드 2였는데, 역시나 여러 가지 아이디어를 생각하다 다른 분의 풀이를 참고해서 해결할 수 있었습니다.

풀이 과정 정리
요새 난이도가 있는 문제 풀이를 잘 안 해서 그런지 풀이를 보고 이해하는 것도 조금 어려웠던 문제입니다.
우선, 처음 문제를 봤을 때는 배열의 특징부터 뽑아 봤습니다.
- A 배열은 대칭 행렬 구조이다.
- A 배열의 대각선 상에 위치한 원소들의 값은 제곱수이다.
- N^2개의 배열 원소 중에서 K번째로 큰 값을 찾으면 된다.
그래서 이렇게 특징들을 뽑고 이분 탐색 방식으로 조건에 맞는 i + j 부터 찾으면 되지 않을까라고 생각했습니다.

왜냐하면, 배열이 이렇게 만들어져 갈 때
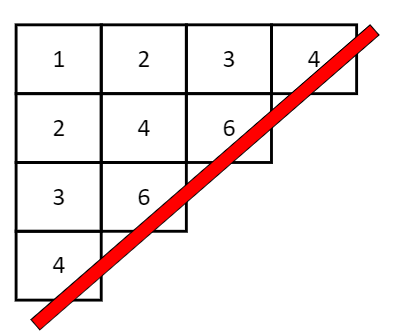
이렇게 대각선 끝쪽에서 안으로 갈수록 값이 커지는 구조를 갖기 때문이라고 생각했습니다.
-> 끝에서 4 x 1 = 4에서 출발 -> 3 x 2 = 6 -> 이런 식으로 진행하고, 이분 탐색으로 대각선으로 개수를 세어 k보다 작으면서 가장 큰 값을 찾아 이걸 대각선 끝 좌표로 삼고 대각선 안쪽으로 진행하면서 찾는다. 이렇게 생각한 것이죠
하지만, 이렇게 푸는 경우 당연하게도 대각선 안쪽으로만 진행해서 찾을 수 없는 중간 값들이 문제가 됩니다.

그래서 다른 분들의 풀이를 참고해 배열이 진행되는 방식을 구구단의 나열처럼 생각할 수 있다는 특징을 발견할 수 있었습니다.
이 부분은 제가 참고한 글의 작성자 분이 너무나도 친절하게 잘 작성해주셔서 저는 제가 알게 된 부분만을 정리해보려 합니다. (자세한 내용은 여기를 참고)

이렇게 배열의 각 값이 A[i][j] = i x j 이므로 가로로 i = 1일 때는 1단, 2일 때는 2단, ..., n일 때 n단 구조로 값이 증가하는 방식의 해석 방식입니다.
이렇게 되면, 우리가 예를 들어 12라는 값보다 작거나 같은 원소의 개수를 다음과 같이 찾을 수 있습니다.
for(int i = 1; i <= n; i++){
count += min((x / i), x);
}여기서 x/i, n 중 작은 수를 고르는 이유는 i단에서 가장 큰 값이 x가 n보다 큰 경우 같은 경우에 올바른 계산을 위해서입니다.
왜 x / i가 각 단에서 x보다 작은 수의 개수를 의미하는지는 마찬가지로 구구단의 개념을 대입해보면 됩니다.
예를 들어) 3단에서 7보다 작은수: 3, 6 -> 7 / 3 = 2 이렇게 구할 수 있기 때문입니다.
이분 탐색 개념
또 문제를 풀기 위해 필요한 이분 탐색에 대해서도 오랜만에 보니 헷갈려서 제대로 짚어서 정리해 봤습니다.
간단하게 이렇게만 생각하자.
- lower-bound: 찾는 값보다 처음으로 크거나 같은 값을 찾는 이분 탐색 방식
- upper-bound: 찾는 값보다 처음으로 큰 값을 찾는 이분 탐색 방식
그래서 코드에서 드러나는 차이점 또한 한 가지입니다.
- lower-bound: 나보다 작은 값을 탐색 범위에서 제외하며 탐색
- upper-bound: 나보다 작거나 같은 값을 탐색 범위에서 제외하며 탐색
long long lower_bound_binary_search(long long k) {
long long start = 1;
long long end = k;
while (start < end) {
long long mid = (start + end) / 2;
// 여기가 다르다.
if (k <= mid) {
end = mid;
}
else {
start = mid + 1;
}
}
return start;
}
long long upper_bound_binary_search(long long k) {
long long start = 1;
long long end = k;
while (start < end) {
long long mid = (start + end) / 2;
// 여기가 다르다.
if (k < mid) {
end = mid;
}
else {
start = mid + 1;
}
}
return start;
}위 코드는 이번 문제를 풀이하며 사용한 코드를 살짝 수정한 이분 탐색 코드입니다.
제출한 코드 (C++)
#include <iostream>
using namespace std;
int n, k;
long long countGugudan(long long x) {
long long cnt = 0;
for (int i = 1; i <= n; i++) {
if (x / i > n) {
cnt += n;
}
else {
cnt += (x / i);
}
}
return cnt;
}
long long binarySearch(long long k) {
long long start = 1;
long long end = k;
while (start < end) {
long long mid = (start + end) / 2;
if (k <= countGugudan(mid)) {
end = mid;
}
else {
start = mid + 1;
}
}
return start;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> n >> k;
cout << binarySearch(k);
return 0;
}
/*
배열 전체를 담을 공간은 프로그램 상에서 만들 수 없다.
따라서 배열을 만들지 않고 문제를 해결해야 한다.
** 배열의 특징 **
1. A 배열은 대칭 행렬이다.
2. A 배열의 대각선 상에 위치한 원소들의 값은 제곱수이다.
3. N^2개의 배열의 원소 중에서 K번째로 큰 값을 찾으면 된다.
4. 2차원 배열을 구구단 표처럼 생각해보자.
5. 그러면, 우리가 수의 값을 기준으로 이분 탐색을 진행할 때, 구구단 표를 보면서 해당 값보다 작은 수를 세는 구조가 된다.
*/참고한 글
https://st-lab.tistory.com/281
[백준] 1300번 : K번째 수 - JAVA [자바]
https://www.acmicpc.net/problem/1300 1300번: K번째 수 세준이는 크기가 N×N인 배열 A를 만들었다. 배열에 들어있는 수 A[i][j] = i×j 이다. 이 수를 일차원 배열 B에 넣으면 B의 크기는 N×N이 된다. B를 오름차순
st-lab.tistory.com
'Algorithm > PS' 카테고리의 다른 글
| BOJ - 3584번, 가장 가까운 공통 조상 [LCA] (0) | 2023.01.17 |
|---|---|
| BOJ - 2792, 보석 상자 매개 변수 탐색 (이분 탐색) (0) | 2023.01.03 |
| BOJ - 1926번, 그림 문제 DFS를 이용한 풀이 (0) | 2022.12.29 |
| BOJ - 14002번, 가장 긴 증가하는 부분 수열 4 문제, LIS 예제와 DP 풀이 (0) | 2022.12.28 |
| BOJ - 2294번 동전 2 문제풀이 (DP, SET 사용) (0) | 2022.12.28 |




댓글