이분 그래프(Bipartite Graph) 란?
이분 그래프(Bipartite Graph)는 그래프의 정점을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있는 그래프를 의미한다고 합니다.
제가 풀이한 백준 1707번 이분 그래프 문제에서는 설명하고 있어 무슨 말인가 싶어 구글링을 통해 찾아본 결과
이분 그래프는 인접한 정점끼리 서로 다른 색으로 칠했을 때 모든 정점을 두 가지의 색으로 칠할 수 있는 그래프이다!
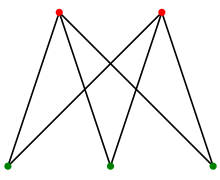
이러한 성질로 인해서 같은 그룹의 정점끼리는 간선으로 연결되지 않고, 간선은 서로 다른 그룹에 대한 정점만을 연결하는 특징을 갖습니다.
참고로 간선 없이 하나의 정점으로 존재하는 그래프 또한 이분 그래프(Bipartite graph)라고 할 수 있습니다!
이분 그래프를 확인하는 방법
이분 그래프를 확인하는 방법에는 대표적으로 두 가지가 있습니다.
- BFS (Breadth-First Search)
- DFS (Depth-First Search)
위 두 개의 대표적인 그래프 탐색 알고리즘을 사용하면, 해당 그래프가 이분 그래프인지 확인할 수 있습니다.
그래프 탐색 알고리즘을 이용해 그래프의 각 정점을 방문하며 2개의 구분자로 정점을 표현하는데, 방문할 때마다 구분자를 바꾸면서 정점을 표현하는 방식을 취하면 됩니다. (마치 2가지 색으로 정점을 칠하는 것처럼)
이렇게 그래프 내의 모든 정점을 탐색하며 별 문제가 없었던 경우 (2개의 구분자로 모든 정점을 표현하는 데 성공한 경우) 이분 그래프로 해당 그래프를 판별할 수 있습니다.
탐색 과정에서 정점을 다른 색으로 바꿔야 한다던가 하는 문제가 발생하면, 이분 그래프라고 판단할 수 없습니다!
✔ 추가적으로 주의해야 할 점은 연결 그래프뿐만 아니라 비연결 그래프 또한 이분 그래프가 될 수 있다는 점입니다! ✔
이분 그래프를 확인하는 예제 코드 (C++)
아래의 예제 코드는 제가 백준 1707번 문제를 풀이할 때 제출한 코드와 동일하니, 이 부분 참고하시면 좋을 것 같습니다!
#include <iostream>
#include <vector>
#include <queue>
#define MAX 20001
using namespace std;
vector<int> m[MAX];
int visited[MAX] = { 0, };
bool BFS(int idx) {
queue<int> q;
q.push(idx);
visited[idx] = 1;
while (!q.empty()) {
int x = q.front();
int cur = visited[x];
q.pop();
for (int i = 0; i < m[x].size(); i++) {
int y = m[x][i];
// 현재 칸의 구분자가 1이면 2, 2이면 1로 할당
int next = (cur == 1) ? 2 : 1;
// 다음 칸의 구분자가 이미 작성되어 있고, 현재 칸의 구분자와 같다면
if (visited[y] == cur)
return false;
// 다음 칸의 구분자가 이미 잘 작성된 경우 건너 띈다.
if (visited[y] == next)
continue;
visited[y] = next;
q.push(y);
}
}
// 위 과정에서 별 이상이 없었던 경우 bipartite graph라고 할 수 있다.
return true;
}
void init() {
for (int i = 1; i < MAX; i++) {
m[i].clear();
visited[i] = 0;
}
return;
}
int main() {
int t;
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> t;
while (t--) {
int v, e;
cin >> v >> e;
init(); // vector 내의 모든 요소를 비운다.
for (int i = 0; i < e; i++) {
int sta, end;
cin >> sta >> end;
m[sta].push_back(end);
m[end].push_back(sta);
}
bool isBipartite = true;
for (int i = 0; i < v; i++) {
if (visited[i] != 0)
continue;
if (!BFS(i))
isBipartite = false;
}
cout << (isBipartite ? "YES\n" : "NO\n");
}
return 0;
}References
https://www.acmicpc.net/problem/1707
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
https://ko.wikipedia.org/wiki/%EC%9D%B4%EB%B6%84_%EA%B7%B8%EB%9E%98%ED%94%84
이분 그래프 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 2색변 이분 그래프의 예 그래프 이론에서 이분 그래프(二分graph, 영어: bipartite graph)란 모든 꼭짓점을 빨강과 파랑으로 색칠하되, 모든 변이 빨강과 파랑 꼭짓점
ko.wikipedia.org
https://gmlwjd9405.github.io/2018/08/23/algorithm-bipartite-graph.html
[알고리즘] 이분 그래프(Bipartite Graph)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
'Algorithm' 카테고리의 다른 글
| LIS (Longgest Increaseing Subsequence)에 대해 이것 저것 정리 (0) | 2023.08.24 |
|---|---|
| 세그먼트 트리 (Segment Tree) 개념 정리 (1) | 2022.11.16 |
| BOJ - 11054번 가장 긴 바이토닉 부분 수열, 동적계획법 문제 (0) | 2022.08.16 |
| BOJ - 1022번 소용돌이 예쁘게 출력하기, 구현 문제 (with C++) (0) | 2022.08.11 |
| BOJ - 2211번 네트워크 복구, dijkstra(다익스트라) 풀이 (C++) (0) | 2022.08.06 |




댓글